Batch 2 - Class 92 - Folding and Pouring, Dots and Dashes

• (Geoffrey - 64) As soon as the news of bank robbery came in, a police car was sent to High Street bridge. The robbers had made their escape in a car, and the bridge was the only point of escape north of town. The police car took strategic position at point A on the map. Three patrols were assigned to patrol A-B, A-D and A-C, each going back and forth the blocks 200mx100m in size, at uniform speed of 10km/hr. All of them started from point A at 4am. On the first occasion thereafter when the three met at the car together, a radio message advised them that the robbers had escaped from south side of town. What time did the message arrive?

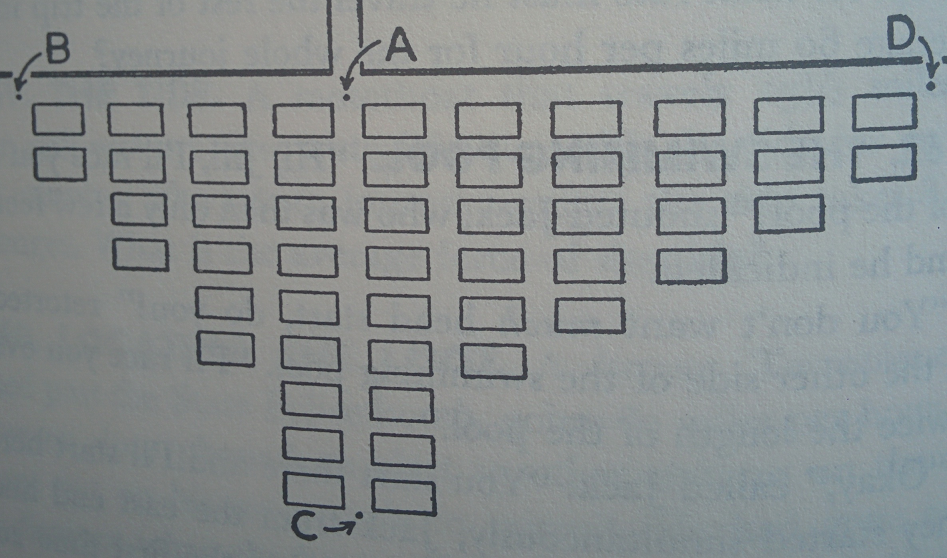
• Answer: Each patrol must have run 72 lengths of blocks, i.e. 14400 metres when they first get together. At 10km/hr, this means about 1:26 hrs, so time must be 5:26 am

• One gallon of water is distributed between two containers labeled A and B. Three quarters of contents of A are poured into B, and then half of contents of B are poured back into A. This process is continued indefinitely. What happens in the long run?

  Instructor Notes: Let kids play around with the problem for some time. Some of them may come up with an approximate answer
• Lets try some paper folding - take a strip of paper and make a crease mark at an arbitrary position. Now make a new crease half way between this position and left end of the strip by folding left end of the strip. Now make a new crease half way between this new mark and right end of the strip. Keep doing this. What happens?

  Kids should be able to come to the conclusion that it starts to alternate to about 1/3 and 2/3 pointsWhy? Can you mathematically explain? Instructor Notes - Try to revisit binary math with kids. Especially post the decimal pointIf the initial crease is at x=0.abcd, where does the left fold bring the crease to? What is binary representation of half of x?Where does the right fold bring it to? What is the binary representation of x+(1-x)/2 = 1/2+x/2?Note that these actions simply insert a 0 and 1 to first slot post decimal. So if we do this indefinitely, what is the sequence we start to get? 0.0101010101... and 0.1010101010..., which is 1/3 and 2/3 respectively!
• Can you see any correlation between our water pouring problem and paper folding problem?

  They are equivalent! So if we transferred half of the water back and forth, we will land up with 1/3 and 2/3 alternates!What if we were transferring 3/4 one way and 1/2 another way? What would happen in binary terms then?Its same as A->B, A->B and then B->A, so 0.100100100... which is 4/7What if we transferred 9/10 back and forth?Hey! this is simple base 10 arithmetic. 0.09090909... and 0.90909090... in decimal is 1/11 and 10/11

• Consider a sequence of square numbers 1, 4, 9, 16, 25 ... Then the sequence of non-square numbers is 2,3,5,6,7,8,10,11... Can you find the 100th non-square number? Can you find a formula for nth non-square number?

  Instructor Notes: Let kids play with this for a bit. Some of them may come to rough approximation that it should be about n+sqrt(n) even though it is not preciseGet to the notion that this might be "off by 1" so perhaps rounding up and down might work
• Consider a list of prime numbers {p(n)}: 2,3,5,7,11,13,17... where p(n) is nth prime. Let q(n) represent number of primes less than n. What is the list {q(n)}

  Answer: {q(n)}: 0,0,1,2,2,3,3,4,4,4,4,5... (Make sure kids understand what this list is)Now make another list of r(n) which is number of items in {q(n)} which are less than nVoila! we get back {p(n)}Why did this happen?Can you create another list which does the same?Advanced: Now create {P(n)} where P(n)=p(n)+n, and {Q(n)} where Q(n)=q(n)+n. What do you observe in these two lists?These two lists exclusively cover all counting numbers!So what would happen if {P(n)} was list of all square numbers? What would {Q(n)} be? How do we construct {P(n)}? What would {p(n)} be? and {q(n)}? Instructor Notes: If kids are unable to construct another list, ask them to try a random list of increasing numbers (numbers can repeat)Why does this hold true for all such lists?At this point, kids may come up with some intuitive explanationsLets try to represent these lists as dots and dashes. For example 1,2,2,2,3,3,6,7,7,7,7,9... is *|*|||*||***|*||||**...What is p(n) in terms of dots and dashes? (Number of dots to the left of nth dash)What is q(n) in terms of dots and dashes? (Number of dashes to the left of nth dot)Notice that the definitions are the same - just "dots" and "dashes" reversed!Instructor Notes: Encourage kids to think about it and absorb itCan you think about what happens when you add n to nth element of the list? What position are we getting now? Why are they unique and cover all countable numbers?

• (Moscow - 235) A dying Roman, knowing his wife was pregnant, left a will saying that if she had a son, the son must get 2/3 of the inheritance and the widow must get 1/3. However, if she had a daughter, the widow must get 2/3 and daughter must get 1/3. Soon after his death, the widow had twins - a son and a daughter. How should the inheritance be divided as close as possible to the terms of the will?

  Answer: There is no single "right" answer:The father's intent is for a son to get twice as the mother, and the mother to get twice as much as the daughter. So you could divide the estate into 7 parts, give 4 to the son, 2 to mother and 1 to daughter.May be the father wished the mother to get at least 1/3, so could give her that. Then the son gets 4 times the daughter on the remaining estate, i.e. 4/5*2/3=8/15One of the twins must have been born first. If its the boy, give him 2/3 and then divide the remaining between widow and daughter in 2:1 ratio. Similarly, if the girl was born first.